Mechanics
Featuring two contributions analyzing the period of pendulums.
The period of a non-ideal pendulum
Author: Justin Wheeler
Abstract: The period of a pendulum swinging at large angles is dependent on the length of the pendulum and the maximum angle at which it swings. This report seeks to measure the validity of the proposed period equation for pendulums swinging at large angles. It has been observed that longer pendulums yield a higher accuracy in the predicted period.
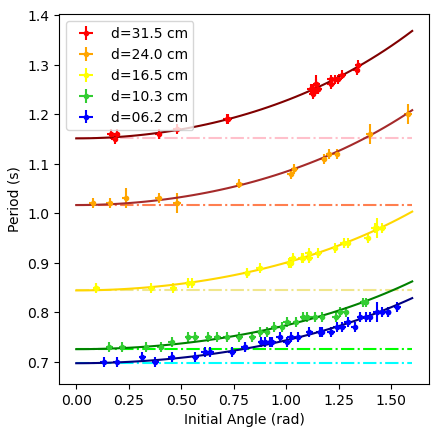
The elliptic relation between release angle and period for a pendulum.
Author: Sophia Figura
Abstract: Two prominent models that give the period of a pendulum are the ideal pendulum, utilizing the small angle approximation, and the non-ideal pendulum, utilizing and elliptic integral. These models were compared against each other for pendulums of varying angles across 5 different pendulum lengths. While the ideal pendulum works well for small angles, its accuracy falls off rapidly as the release angle of the pendulum is increased. The elliptic model, while harder to work with, maintains its accuracy at both large and small angles.